こんにちは、京大生ゆーはです。今回は私が京都大学経済学部にて専門的に勉強しているミクロ経済学について、簡単な例題を使って紹介します。
専攻 ミクロ経済学の典型的な例題
ミクロ経済学は個人の経済に焦点を当ててその最適化や意思決定などを主に偏微分を用いて考えます。
いきなりですが、雰囲気をつかんでもらうため、具体的な問題を用意しました。
「あなたの月収入12万のうち、いくら貯金すれば幸福度が高いでしょうか？」
これを幸福度を示す数式で仮定義してそれを解きます。自分の感じる幸せの量(経済学では効用と定義する)をUと置き、U=x²yと表せると仮定して、貯蓄x円,支出y円の理想を計算します。
————————————————————————————–
今月のあなた(大学生)の貯蓄額をx,支出額をy、親からの仕送り額を12(万円)とする。
効用U=x²yとしたときに、Uを最大化するx.yを求めよ。
例えば、12万円のうち半分を支出、半分を貯蓄に回した時、効用U=216である。
————————————————————————————–
このような問題を微分を使用して解くことができます。
<解き方>
この問題はx+y=12(x>=0, y>=0)(予算制約) と表せることから
y=12-xをU=x²yに代入すると、U=x²(12-x)=-x³+12x²
について偏微分を行うことによって、Uを最大化するxを求めることができる。
∂U/∂x=-3x²+24x よりx＝8、の時に∂U/∂x=0 (x=0の時も該当するが、U=0となるので違う)
この時、y=4 U=256
この計算自体は高校生レベルの連立方程式である。
なぜ微分で解けるのか
与えられた計算では、U,x,yと記号が3つも出てきて計算しにくい。
そこで予算の制約から、x+y=12と表せることを利用して、Uとxの式に持っていく。
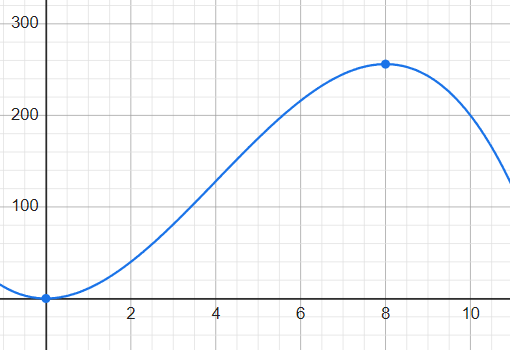
すると、U=-x³+12x²の式が以下のグラフのようになり、縦軸Uが最大化する部分は一目瞭然。微分することで、接線の傾きが0の部分を求めることになるので、x=0, 8が出てくる。
つまり、微分した後に、その値が適しているのかを確認する必要はある。
このミクロ経済学の何が面白いのか
問題をただ解くというのも私は嫌いではありませんが、実践的ではなく面白くないと思う人も多いと思います。
では面白みはどこにあるのか。
それは、自分でイチから効用Uの式を作っていくことにあります。実際の事例に当てはめると効用を左右する要素がたくさん出てくるので、とても複雑にはなります(上の例でも「貯蓄がもともとどれくらいあるのか」「仕送り以外の収入源はあるのか」などで変わってきます)。
余すことなく、要素を拾っていって感覚的な部分と相違ないことも確認していきます。
実は今回の例題も私自ら作成しました。支出8~10万くらいかなという回答ありきで何度か修正しました。
日頃の思考で立式まではしなくても、例えば「支出がかなり増えている時の心理的背景は何があるかな？仕事のストレス？衣替え時期？」など影響を与える要素を拾ってくる力になっている気がしています。
他にも「1か月の中で、私にとって最も幸福度が高くなるような外食の回数は？」「親しいと思える人の人数と幸福度の関係は？」など自分の感覚に合うような計算式を模索してみるのも面白いかもしれません。ただし、一般的には2~4次関数までで立式を組み立てるのが現実的かと思います。
実際に専門的になってくると、「マラリアの予防接種を打たない行動の要因分析」として行動経済学の中で数式に落とし込むようなことをしたことがあるのですが、要素が多すぎるため難しくて、でてきた数式を見ると頭がおかしくなります(これは要因分析だけで微分とかはしません)。
ミクロ経済学を応用した考え方
普段の生き方や幸せについてもこのミクロ経済学を応用して考察した記事を書いています。ここでも同様に効用についての解説から始めていますので、どのように落とし込んでいるのかぜひのぞいてみてください。
まとめ
経済学は文系の学部なので、あまり数式を使うような分野は敬遠されがちです。しかし、実生活との結びつきを意識することでかなり身近に感じることができると思います。
ちなみにそもそも支出管理すらしていなかったという方は、私の作った家計簿エクセルファイルがありますのでぜひ覗いてみてください。https://kyodaiseiyuha.com/京大経済学部生の家計簿紹介/
この記事で少しでもミクロ経済学の魅力を持っていただけると幸いです。
Thank you for your reading!!
